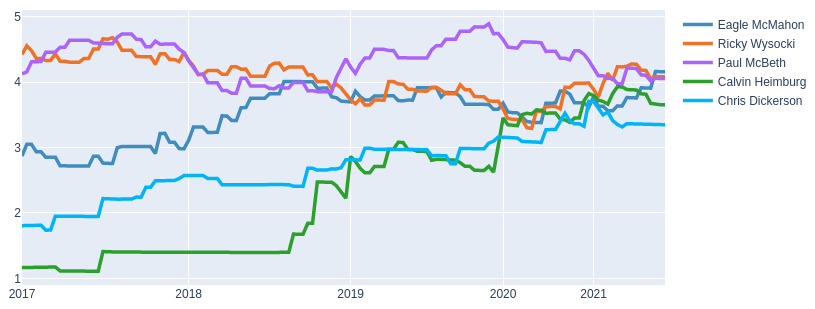
With the unveiling of Disc Golf World Rankings powered by UDisc, we wanted to peel back the curtain and give fans and stat-heads a detailed explanation of how the system works. If the existence of this system is news to you, we suggest you give our article "Introducing Disc Golf World Rankings" a read before continuing with this one.
Creating a system that accurately ranks the best professional disc golfers in the world was an intensive, iterative process from conception to finished product. Here are some of the core questions that guided the design process:
- How can we align incentives with what the pros are trying to do – win the tournament?
- Should we set a laser focus on the best of the best – the top 10 players from each division – or give equal consideration to every touring pro?
- How sensitive should the system be to each subsequent event?
- Should the ranking list start from scratch every season or roll over into the next?
As the answers to those questions gradually revealed themselves, we carefully designed a model which we hope will fit all the nuances of our favorite sport.
If you just want to know what the formulas are and how to apply them, keep reading – we'll cover that right away. If that whets your appetite, we'll also explain some of the math that justifies the formulas and show how the system's accuracy can be measured and optimized.
On the Shoulders of Giants
The Disc Golf World Ranking system is based on the Elo rating system for chess. In that system, each chess player maintains a rating – a number between 100 and 3000 – which fluctuates depending on match results. There are many equivalent ways to formulate the Elo update rule; here is one of them. Let r1 and r2 be the initial rating of the winner and loser of a chess match, respectively. Their new ratings, r1' and r2', are calculated according to the formulas

where k is a constant which determines how big of an effect each subsequent match can have. New players typically start with a rating close to 1500. For those familiar with Elo, the above formulas may look somewhat different from the way they are usually presented. You are encouraged to check that they really are the same!
The main challenge in adapting Elo to disc golf is that Elo only works for two-player (or possibly two-team) games while disc golf is a many-player game. UDisc is not the first to attempt an adaptation; our friends over at Ultiworld Disc Golf experimented with an Elo adaptation for disc golf for the 2017 season. UDisc's system uses a brand-new, custom-made adaptation designed from the ground up for multiplayer games.
The Formula
UDisc has departed from the traditional Elo rating scale which was designed to roughly match the scale of its predecessor, the Harkness rating system. Instead of using the exponential base of 101/400, we use the natural exponential base of e ≈ 2.718. Each player's rating can be positive, negative, or zero, with new players starting at a rating of 0, and the average rating of active players being maintained at 0 (a player is considered to be active if they have played at least one event in the last two years). Since new or inactive players' ratings aren't guaranteed to be accurate, we protect active players by performing their rating updates as if inactive players didn't exist.
We will be using the word "rating" a lot in this article. This refers to UDisc's Elo-style rating and should not be confused with the PDGA rating system.
After an event with n players has concluded, order the ratings of the players according to their finishing position. That is, let r1 be the rating of the winner, r2 the rating of the second-place finisher, and so on until the last place finisher with rating rn. For now, let's consider the ideal situation where there are no ties. The rating update for the player finishing in position i is given by the equation

In the above equation, ri' is the player's new rating, exp is the exponential function, and k is a constant which determines how big of an effect each subsequent event can have. We use k = 0.15 for MPO and k = 0.25 for FPO (we'll show you how we decided on these values later in the article).
To wrap your head around the updating formula, imagine that you are the player in question. The number of terms in the outer summation above is equal to the number people that you beat plus one – yourself. These terms all contribute positively to your rating update, so finishing better always results in a more favorable update. For a given q with q ≥ i, the lower your rating, the larger the expression

This means that, given your finishing position, a lower initial rating results in a more favorable update than having a higher initial rating.
Let's do an example to solidify our understanding. Suppose there is a four-person tournament between players A, B, C, and D with initial ratings 2.0, 0.1, -0.1, and -2.0, respectively. Suppose further that player A wins the tournament, followed by player D, then player C, and finally player B. The update procedure is illustrated in the table below.
| Player | Initial Rating (ri) | Terms of the Sum | Subtotal | Subtract 1 | Multiply by k = 0.15 | Final Rating (ri') |
| A | 2.0 | 0.014 + 0.016 + 0.018 + 1 | 1.048 | 0.048 | 0.007 | 2.007 |
| D | -2.0 | 0.775 + 0.856 + 0.982 | 2.613 | 1.613 | 0.242 | -1.758 |
| C | -0.1 | 0.116 + 0.128 | 0.244 | -0.756 | -0.113 | -0.213 |
| B | 0.1 | 0.095 | 0.095 | -0.905 | -0.136 | -0.036 |
Let's make some observations. Player A won the tournament, but they were by far the favorite. Their rating increases but just barely. Player D is just the opposite: They entered the tournament with the lowest rating but managed to place second. Therefore their rating increases significantly. Player C is perhaps the most interesting. They entered the tournament with the third best rating and came in third place. In particular, they lost to player A (as expected), they upset player B, and were upset by player D. Player C's rating decreases because their rating difference with player D was more extreme than their rating difference with player B.
Random Variables and Gradient Descent
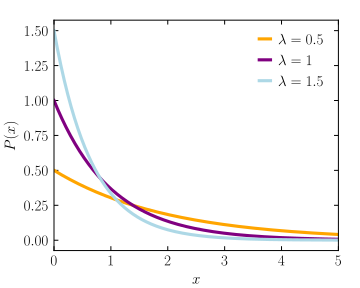
Now that we know how the updating formula works, let's explore why it works. The core component is the statistical notion of a random variable. The short version is that we represent a player's skill not with a single number, but with an entire probability distribution. After all, on a given day, each player may perform somewhat better or worse than their true strength. For a player with rating r, we represent that player by an exponential random variable with rate parameter λ=exp(-r). Thus, a player with a higher rating has a lower rate parameter, and therefore a higher probability of performing well (see the figure below).
The next ingredient which goes into the updating formula is an idea called stochastic gradient descent (which we'll abbreviate as SGD). Picture yourself in a dense fog on the side of a hill. You know that somewhere below you, at the very bottom of the valley, there is a tavern. How can you get to the tavern even though you can't see more than a couple feet in front of you? Well, you should always go downhill. In fact, if you want to get to the tavern as fast as possible, a good strategy would be to take a step in the direction where the slope of the hill is steepest. In this analogy, there are two variables controlling which direction you take each step: North/South and East/West. These two variables are called weights. Your goal is to get to the bottom of the valley, that is, to minimize your altitude. Your altitude is called the objective function.
To use SGD to update each player's rating, it is necessary to define the weights and the objective function. The weights are the ratings of each of the players (so in a tournament with n players, imagine standing on an n-dimensional hill!). The objective function we'll use is called cross-entropy loss. The short version is that in an event with n players, there are n factorial different possible outcomes. Since each player is represented by a random variable, it is possible to compute the probability of each outcome, and we get a better score according to cross-entropy loss if we assigned a higher probability to the actual outcome of the event. In fact, if r1 is the rating of the player who finished first, r2 the rating of the player who finished second and so on, then the formula for cross-entropy loss is given by

To determine which direction to step on our n-dimensional hill, we need to figure out the gradient (i.e., steepness) of the hill in each direction. Mathematically, this means computing the partial derivative of the objective function with respect to each of the weights. Doing this requires some knowledge of calculus and a lot of patience, but the answer at the end of the day is

This expression might look familiar. It is actually the parenthetical expression from the updating formula at the beginning of the article! To complete the formula, we drop the minus sign (because we want to go down the hill rather than up the hill), multiply by k (remember this is 0.15 for MPO and 0.25 for FPO) which represents the size of the step, and add the result to the initial rating.
Fine-tuning
So why k = 0.15 for MPO and k = 0.25 for FPO? To arrive at these values, we had to evaluate how accurate our ranking system was. To be more specific, we can consider the initial player rankings before each event to be a prediction of the event outcomes and use various metrics to determine the predictive power of the system. The value of k which maximizes the predictive power of the system is the one we went with. Here are the metrics we used to evaluate the system:
- Top 10% — Predict which players will finish in the top 10% of the field (rounded up). The value of this metric is the proportion of those players who actually did finish in the top 10%. Higher is better with a perfect score of 1 and a worst possible score of 0.
- Top 50% — Similar to above, predict which players will finish in the top half of the field (rounded up). The value of this metric is the proportion of those players who actually did finish in the top half. Higher is better with a perfect score of 1 and a worst possible score of 0.
- Inversion Average — Consider the event as several head-to-head match-ups and predict which player wins each match-up. The value of this metric is the proportion of total match-ups which are upsets (the worse ranked player wins). Lower is better with a perfect score of 0 and a worst possible score of 1.
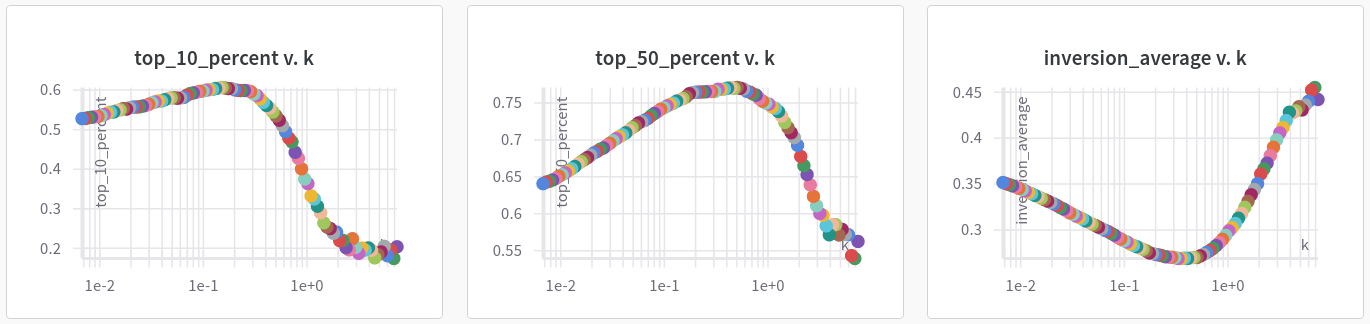
We simulated the ranking system 100 times using values of k on a logarithmic scale between 0.007 and 7. Here are the results for MPO...
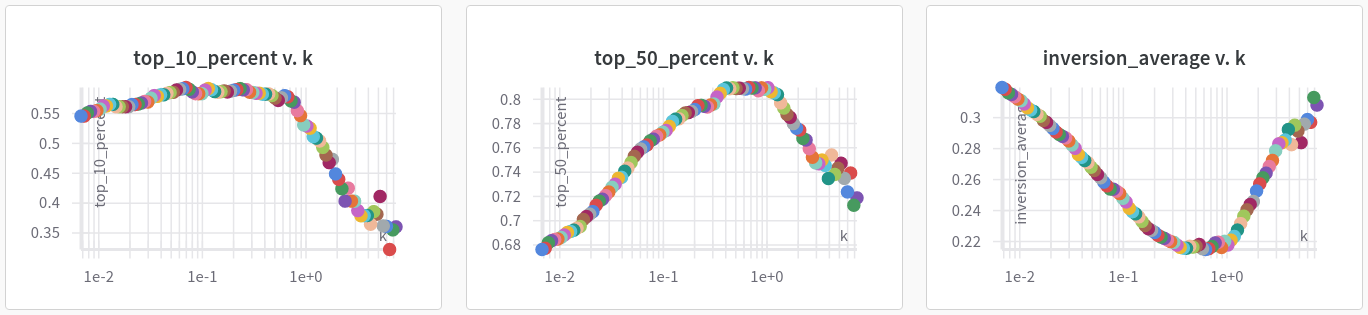
...and FPO
It's a bit hard to make out, but the Top 10% metric maxes out at around k = 0.15 for MPO and k = 0.25 for FPO (the FPO graph has a bit more noise, but we follow the general trend here). The Top 50% and Inversion Average metrics are actually optimized at slightly larger values of k. We decided to use the smaller value of k (the one which maximizes the Top 10% metric) because we wanted the focus to be on the cream of the crop – the very best players in the world. This has the added qualitative benefit of placing slightly less importance on each subsequent event so that the system isn't totally reactionary.
The table below shows the current average values of the metrics on qualifying events from 2017 onward. Also included for fun is the "Winner" metric which is the proportion of times the system accurately predicted the winner of an event.
| Metric | MPO | FPO |
| Top 10% | 0.5908 | 0.6031 |
| Top 50% | 0.7572 | 0.8295 |
| Inversion Average | 0.2741 | 0.2016 |
| Winner | 0.3750 | 0.5803 |
The standout figure here is that the system accurately predicted the winner of FPO events a little over 58% of the time. This is a testament to how much of a no-brainer it is to bet on Paige Pierce!
Dominance Index – The Nitty Gritty
As explained in our article "Introducing Disc Golf World Rankings," Dominance Index provides a way to compare the probability of each player winning in a head-to-head match-up. For a player with rating r, their dominance index is given by D = exp(r). You can use Dominance Index to determine the probability of each player winning among a group of players though the formula gets more complicated than the two-player case. You don't need to do the math because we've done it for you in our player comparison tool! If you still want to know the formula (if you've read this far, you probably do), here it is.
For a group of n players with Dominance Indices D1, D2, ..., Dn, let λk = 1/Dk. The probability that player k wins is given by

where [n]-k denotes the set of integers 1 through n excluding k, the outer summation is over all subsets of these numbers, and |S| is the size of the subset.
There is more to come! Keep an eye out for announcements about new additions to UDisc Live, the UDisc app, and UDisc online here on Release Point or make sure to never miss one by signing up for our twice-monthly newsletter.